En virtud de las dificultades que noto para la construcción de perpendiculares y bisectrices, les dejo dos videos para que los miren las veces que crean necesarias hasta poder hacerlo correctamente.
Perpendicular a un segmento dado
Bisectriz y mediatriz
En este último enlace se repite el procedimiento para realizar la perpendicular que pasa por el punto medio del segmento dado, la cual se llama mediatriz.
Practiquen estos procedimientos con los ejercicios que están publicados desde la semana anterior.
"Un gran descubrimiento resuelve un gran problema, pero en la solución de cualquier problema hay una pizca de descubrimiento. Tu problema puede ser modesto, pero si es un reto para tu curiosidad y hace que entren en juego tus facultades de inventiva, y si lo resuelves con tus propios medios experimentarás la tensión y gozarás el triunfo del descubrimiento." George Polya
sábado, 27 de abril de 2013
miércoles, 24 de abril de 2013
Definiciones geométricas (1° a 6°)
Les dejo algunas definiciones importantes para la geometría plana.
Punto: Es lo que no tiene partes (se representa geométricamente para hacer
referencia)
Recta: Es una sucesión indefinida de puntos en una misma dirección. No
tiene ni principio ni final.
Semirrecta: Es una línea recta que tiene principio pero no final.
Segmento: Es la parte de una recta comprendida entre dos puntos.
Rectas secantes: Dos rectas son secantes cuando tienen un
punto en común (se cruzan en un punto).
Rectas paralelas: Dos rectas son paralelas cuando no tienen
ningún punto en común (nunca se cruzan).
Rectas coincidentes: Dos rectas son coincidentes cuando tienen
todos sus puntos en común.
Rectas perpendiculares: Dos rectas son perpendiculares cuando al
cortarse forman cuatro ángulos iguales de 90º.
Mediatriz: Es el segmento perpendicular a un segmento dado, que pasa por el punto
medio del mismo.
Vértice: Es el punto donde dos o más rectas se cruzan.
Ángulo: Es cada una de las porciones en que queda dividido el plano cuando se
cruzan dos rectas secantes.
Ángulo agudo: Es un ángulo menor de 90º.
Ángulo recto: Es un ángulo de 90º.
Ángulo obtuso: Es un ángulo mayor de 90º.
Bisectriz: Es la recta que al pasar por el vértice de un ángulo dado, lo divide en
dos partes exactamente iguales.
Polígono: Un polígono es una porción de plano limitada por tres o más líneas
rectas no paralelas entre sí. Los laterales del polígono se llaman lados y el
punto donde se cruza cada par de rectas se llama vértice. Puede ser regular o
irregular.
Polígono regular: Es un polígono que tiene todos sus lados y
todos sus ángulos iguales.
Polígono irregular: Es un polígono que no tiene ni todos sus
lados ni todos sus ángulos iguales.
Diagonal: Es el segmento de recta, comprendido entre dos vértices no consecutivos
de un polígono de cuatro o más lados.
Altura: Es la distancia entre un lado de un polígono y el vértice opuesto, en
dirección perpendicular.
Triángulo: Es un polígono de tres lados.
Triángulo equilátero: Es
un triángulo que tiene los tres lados iguales.
Triángulo isósceles: Es un
triángulo que tiene dos lados iguales y uno desigual.
Triángulo escaleno: Es un
triángulo que tiene los tres lados desiguales.
Triángulo acutángulo: Es
un triángulo que tiene los tres ángulos agudos.
Triángulo rectángulo: Es
un triángulo que tiene un ángulo recto y los
otros dos agudos.
Triángulo obtusángulo: Es
un triángulo que tiene un ángulo obtuso y los otros dos agudos.
Apotema: Es el segmento de recta que va desde el centro de un polígono regular al punto
medio de uno de sus lados.
Polígonos regulares (1°)
En clase les comenté que las figuras planas que están formadas por segmentos de recta se llaman polígonos. Y en particular, cuando esos segmentos (que llamamos lados) tienen la misma longitud, se llaman polígonos regulares. Veamos algunos ejemplos...
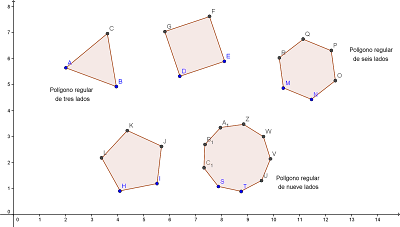
Además armamos una tabla que deben completar. Aquí va la ayuda para la columna "Valor del ángulo interior".
Ya sabemos cuánto suman los ángulos interiores de cualquier triángulo (180°). Entonces, si pudiéramos dividir cualquier polígono en triángulos, podríamos analizarlos mejor, vean cómo se hace con el polígono MNOPQ de seis lados (también llamado hexágono):
Al unir los vértices formamos 4 triángulos, si cada uno suma 180°, entonces 180° x 4 = 720°. Y como la figura tiene 6 lados, decimos 720° / 6 = 120°. Con el mismo procedimiento lograrán averiguar cuánto miden los ángulos interiores de los demás polígonos. De esa manera completarán la columna indicada con los valores correspondientes.
Se pide que copien este ejemplo en la carpeta y que durante la clase del jueves 25/4 realicen lo indicado.

Además armamos una tabla que deben completar. Aquí va la ayuda para la columna "Valor del ángulo interior".
Ya sabemos cuánto suman los ángulos interiores de cualquier triángulo (180°). Entonces, si pudiéramos dividir cualquier polígono en triángulos, podríamos analizarlos mejor, vean cómo se hace con el polígono MNOPQ de seis lados (también llamado hexágono):
Al unir los vértices formamos 4 triángulos, si cada uno suma 180°, entonces 180° x 4 = 720°. Y como la figura tiene 6 lados, decimos 720° / 6 = 120°. Con el mismo procedimiento lograrán averiguar cuánto miden los ángulos interiores de los demás polígonos. De esa manera completarán la columna indicada con los valores correspondientes.
Se pide que copien este ejemplo en la carpeta y que durante la clase del jueves 25/4 realicen lo indicado.
Saludos del profesor
jueves, 11 de abril de 2013
Puntos notables en triángulos
Les dejo este enlace donde encontrarán la teoría y ejercicios respecto al tema Puntos Notables.
Lean la teoría y realicen todos los ejercicios propuestos en hoja aparte para ser evaluados.
En la página que aquí se enlaza pueden ver la ubicación de cada punto en un triángulo al que podrán cambiar forma y tamaño para una mejor interpretación.
Lean la teoría y realicen todos los ejercicios propuestos en hoja aparte para ser evaluados.
En la página que aquí se enlaza pueden ver la ubicación de cada punto en un triángulo al que podrán cambiar forma y tamaño para una mejor interpretación.
jueves, 4 de abril de 2013
Perpendiculares y bisectrices (3°)
Estuvimos viendo como trazar la perpendicular que pasa por el punto medio de un segmento dado.
Luego vimos como hacerlo con los segmentos que forman un triángulo. Dichas perpendiculares se cruzan en un punto y ustedes averiguarán cómo se llama ese punto. Además ¿cómo se llaman esas perpendiculares construidas?
En el siguiente enlace se muestra como se hacen paso a paso: Perpendiculares
También vimos como trazar las bisectrices de los ángulos del triángulo y ustedes averiguarán cómo se llama la triple intersección de las bisectrices. ¿Cómo se llaman esos segmentos?
Ahora les pediré que a otro triángulo le ubiquen los puntos medios de sus lados y tracen los segmentos que unen cada punto medio con el vértice opuesto. Averigüen cómo se llama ese punto de intersección. ¿Cuál es el nombre de los segmentos trazados?
Aún no les dije como trazar la perpendicular a un segmento que pase por un determinado punto exterior a ella (al hacerlo en un triángulo, donde se traza la perpendicular a cada segmento que pasa por el vértice opuesto se llama "altura"). Lo veremos la próxima clase, pero igualmente los desafío a investigar, sorprenderme, intentar hacerlo ustedes mismos y ganarse una buena nota.
Luego vimos como hacerlo con los segmentos que forman un triángulo. Dichas perpendiculares se cruzan en un punto y ustedes averiguarán cómo se llama ese punto. Además ¿cómo se llaman esas perpendiculares construidas?
En el siguiente enlace se muestra como se hacen paso a paso: Perpendiculares
También vimos como trazar las bisectrices de los ángulos del triángulo y ustedes averiguarán cómo se llama la triple intersección de las bisectrices. ¿Cómo se llaman esos segmentos?
Ahora les pediré que a otro triángulo le ubiquen los puntos medios de sus lados y tracen los segmentos que unen cada punto medio con el vértice opuesto. Averigüen cómo se llama ese punto de intersección. ¿Cuál es el nombre de los segmentos trazados?
Aún no les dije como trazar la perpendicular a un segmento que pase por un determinado punto exterior a ella (al hacerlo en un triángulo, donde se traza la perpendicular a cada segmento que pasa por el vértice opuesto se llama "altura"). Lo veremos la próxima clase, pero igualmente los desafío a investigar, sorprenderme, intentar hacerlo ustedes mismos y ganarse una buena nota.
Ángulos (1°)
Antes de ir a los ejercicios, recordemos que los ángulos pueden ser AGUDO, RECTO u OBLÍCUO ¿qué es lo que define esa clasificación?
Les propongo que realicen las siguientes figuras ayudándose con el transportador y la regla:
a) Un triángulo que tenga un ángulo interno de 40°, otro de 50°. El restante ángulo deberán medirlo para conocerlo. ¿Cuánto suman los tres ángulos? (Ayuda)
b) Otro cuyos ángulos internos sean de 50°, 60° y el último lo miden ustedes. ¿Cuánto suman los tres?
c) Otro triángulo al que ustedes pondrán los grados que decidan. ¿Cuánto suman los tres?
d) Finalmente hagan un triángulo sin importar la forma y midan los tres ángulos internos. ¿Cuánto suman? ¿Encontraron alguna coincidencia?
Además de hacer los ejercicios, les pido que repasen ángulos complementarios y ángulos suplementarios ya que lo necesitarán para las próximas clases.
Les propongo que realicen las siguientes figuras ayudándose con el transportador y la regla:
a) Un triángulo que tenga un ángulo interno de 40°, otro de 50°. El restante ángulo deberán medirlo para conocerlo. ¿Cuánto suman los tres ángulos? (Ayuda)
b) Otro cuyos ángulos internos sean de 50°, 60° y el último lo miden ustedes. ¿Cuánto suman los tres?
c) Otro triángulo al que ustedes pondrán los grados que decidan. ¿Cuánto suman los tres?
d) Finalmente hagan un triángulo sin importar la forma y midan los tres ángulos internos. ¿Cuánto suman? ¿Encontraron alguna coincidencia?
Además de hacer los ejercicios, les pido que repasen ángulos complementarios y ángulos suplementarios ya que lo necesitarán para las próximas clases.
lunes, 1 de abril de 2013
El número de Euler (1°)
Estudiaremos algunos cuerpos geométricos para deducir la relación de Euler. En la carpeta deben copiar la tabla (que completaremos el jueves en clase), dibujar el tetraedro y el cubo y luego armar con papel o cartulina el octaedro, el dodecaedro y el icosaedro. Los mejores constructores tendrán nota de premio.
N° de caras (c)
|
N° de vértices (v)
|
N° de aristas (a)
|
N° de Euler= c+v-a
| |
Tetraedro
|
4
|
4
|
2
| |
Cubo
|
6
|
8
|
12
| |
Octaedro
| ||||
Dodecaedro
| ||||
Icosaedro
|
Suscribirse a:
Comentarios (Atom)
