Polígonos regulares (1°)

En clase les comenté que las figuras planas que están formadas por segmentos de recta se llaman polígonos. Y en particular, cuando esos segmentos (que llamamos lados) tienen la misma longitud, se llaman polígonos regulares. Veamos algunos ejemplos...

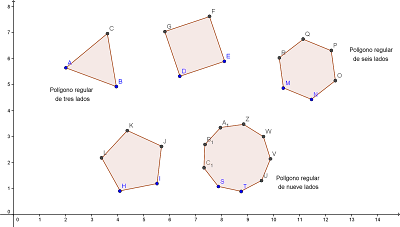
Además armamos una tabla que deben completar. Aquí va la ayuda para la columna "Valor del ángulo interior".
Ya sabemos cuánto suman los ángulos interiores de cualquier triángulo (180°). Entonces, si pudiéramos dividir cualquier polígono en triángulos, podríamos analizarlos mejor, vean cómo se hace con el polígono MNOPQ de seis lados (también llamado hexágono):

Al unir los vértices formamos 4 triángulos, si cada uno suma 180°, entonces 180° x 4 = 720°. Y como la figura tiene 6 lados, decimos 720° / 6 = 120°. Con el mismo procedimiento lograrán averiguar cuánto miden los ángulos interiores de los demás polígonos. De esa manera completarán la columna indicada con los valores correspondientes.
Se pide que copien este ejemplo en la carpeta y que durante la clase del jueves 25/4 realicen lo indicado.

Saludos del profesor