Temas de los examenes

Estimados alumnos, quienes se llevaron la materia deben repasar todo lo visto en clase.
La mayor parte de los temas dados están publicados aquí. Algunos fueron dados sólo en clase y el registro lo tienen en sus carpetas.
Los temas los encontrarán en la columna de la derecha organizados por el mes en que se dieron.
Los programas de primer y tercer año fueron publicados en marzo (ver "organización de los ejes").

Los espero en las fechas previstas (publicadas en cartelera de la escuela) y durante esta semana haremos una revisión para ayudarlos a recordar cada tema. No duden en consultar el blog las veces que quieran.

Estoy para ayudarlos a aprender, asique también pueden consultarme por mail a profesor.rubencejas@live.com.ar

Saludos.

Combinatoria - Combinaciones (3°)

Hasta el momento trabajamos con la parte de la combinatoria a la que le importa el orden de los elementos. En esta oportunidad veremos qué hacer si no importa el orden.
Veamos un esquema, llamado diagrama de flujo.



En un diagrama de flujo se sigue, como su nombre lo indica, el flujo de información. Es muy útil para diseñar o analizar situaciones problemáticas.

Luego del comienzo (com) nos preguntamos ¿importa el orden? En verde se destaca la salida negativa, que es lo que nos importa hoy.

Un ejemplo siempre aclara:

Si me dan a elegir entre seis ingredientes para hacer una ensalada y yo la quiero con cuatro ingredientes (por ej. zanahoria, lechuga, tomate y huevo duro). Claramente no importa el orden en el que incorpore los elementos a la ensalada.

Entonces podemos decir que busco combinar 4 elementos tomados entre 6 opciones.

En principio será como una variación. Pero así estamos contando las permutaciones entre los cuatro elementos elegidos (que es 4!), asique al descontarlas quedará:

         6!          =      6*5*4*3*2*1    

(6-4)! * 4!         2*1 * 4*3*2*1

Esto puede parecer complicado, pero con algunos ejercicios que sean analizados, quedará mucho más claro. Por eso propongo que intenten realizar ustedes mismos el siguiente, como tarea y siguiendo el ejemplo dado:

1. En el coro de una escuela, participan 18 chicas y 9 chicos. El director de dicho coro debe elegir 4 voces masculinas y 5 voces femeninas para interpretar una canción.

    a. ¿De cuántas maneras puede seleccionar el director las voces masculinas?

    b. ¿Cuántas elecciones de voces femeninas puede realizar el director?

Triángulo de Pascal o Tartaglia - Binomio de Newton (3°)

Hace algunas clases conocimos el Triángulo de Tartaglia ó de Pascal. Las filas se numeran comenzando por cero que es la de arriba de todo.
Vimos que los resultados son en definitiva caminos posibles de una moneda o pelotita que cae optando por un lado o el otro de cada "clavito" (pensando a cada número como un clavo) y se dedujo que cada valor es la suma de los dos superiores, como se ve a continuación:

http://unidad-conjuntos.wikispaces.com/Tri%C3%A1ngulo+de+Pascal

Uno de los usos es el que vimos en clase, como herramienta para resolver el conocido binomio de Newton donde el número de fila es la potencia de dicho binomio y los valores intermedios.
Veamos unos ejemplos:

(a+b)² = a² + 2 ab + b²

(a+b)³ = a³ + 3 a²b + 3 ab² + b³

(a+b)⁴ = a⁴ + 4 a³b + 6 a²b² + 4 ab³ + b⁴

Los extremos del desarrollo son los valores a y b elevados a la potencia que se indique, mientras los coeficientes de las distintas potencias tienen directa relación con los valores del triángulo.

Ejercicio:
1. Expliquen con sus palabras la relación existente en el desarrollo respecto a las potencias de cada término.
2. Desarrollar  (a+b)⁵ y (a+b)⁶.

Como ayuda les dejo este enlace que les agilizará la construcción del Triángulo de Pascal/Tartaglia con las filas que quieran: http://www.estadisticaparatodos.es/triangulo

Combinatoria - Variaciones sin repetición (3°)

Se les dió un ejercicio similar al que sigue y ustedes intentaron resolverlo. Veamos otro.

Imaginen que tienen una bolsa oscura (no se puede ver lo que hay dentro) que contiene 8 bolitas numeradas del 1 al 8.
Si se extraen tres bolitas de a una por turno y sin mirar: ¿Cuántos números de tres cifras pueden armarse con dichas extracciones?

Analicemos la situación y hagamos algunos supuestos:
1. Al sacar la primera, puede salir cualquiera de los 8 números.
2. Al sacar la segunda, puede salir un número entre 7 posiblidades, ya que saqué la primera antes y no la repuse.
3. Por lo mismo, al sacar la tercera tendré 6 bolitas númeradas para elegir al azar.

Luego de este breve análisis podemos arribar a una posible solucíón: 8 * 7 * 6 elecciones posibles hacen un total de 336 posibles números de tres cifras. Con el objetivo de asegurarse de lo que digo (siempre duden de lo que se les dice, asegúrense ustedes mismos), les pido que escriban todos los posibles números de tres cifras que contienen al número 1 en alguna posición (unidad, decena o centena).

La situación expuesta es parecida a una permutación, pero de NO TODOS los elementos. Ésto se llama variación de 8 elementos tomados de a 3. Se escribe V_{8; 3} y su fórmula es la siguiente:

V_8;3 =  8!   =  8 * 7 * 6 * 5 * 4 * 3 * 2 * 1

5!            5 * 4 * 3 * 2 * 1

El número 5 surge de restar 3 al 8.

Llamamos variación sin repetición de m elementos tomados de a n, a cada forma de ordenar m elementos en n lugares, sin que un mismo elemento pueda ubicarse en más de un lugar. Se calcula de la siguiente manera:

V_{m; n} =     m!             con m > n

(m-n)!             

Ejercicio: 

¿Qué sucedería en el caso que m = n en la fórmula dada?

Combinatoria - Permutaciones (3°)

En estas semanas estuvimos aprendiendo conceptos muy útiles para el conteo de situaciones que pueden ocurrir en cualquier ámbito.
Comenzamos analizando el juego del "Sudoku" básico. El mismo es una matriz de tres por tres en el que se colocan los números del 1 al 9 y cada fila, cada columna y cada diagonal deben sumar 15.
Por consiguiente se propuso armar ternas que sumaran 15 con el conjunto dado. Así, ustedes armaron todas las ternas que puedieron, respetando las condiciones que no se repitan números y que estén ordenadas de menor a mayor.

Conjunto A={1, 2, 3, 4, 5, 6, 7, 8, 9}

Ternas de A que comienzan con 1 y suman 15: {1; 5; 9}, {1; 6; 8}
Ternas de A que comienzan con 2 y suman 15: {2; 4; 9}, {2; 5; 8}, {2; 6; 7}
Ternas de A que comienzan con 3 y suman 15: {3; 4; 8}, {3; 5; 7}
Ternas de A que comienzan con 4 y suman 15: {4; 5; 6}

Con las condiciones dadas, no hay más ternas. Y esas condiciones son necesarias para evitar confundirse.
A continuación, con cada terna queremos saber de cuántas maneras las podemos utilizar. Es decir, que con la terna {1; 5; 9} podemos hacer otras: {1; 9; 5}, {5; 1; 9} y otras (completar). ¿Cuántas son? En este caso, por ser pocos números, haciendo una lista se deduce fácilmente. Pero si fueran muchos se complicaría un poco. Entonces analicemos.

Los números {1; 5; 9} se deben ubicar en los lugares correspondiente a unidad, decena y centena. Veamos: para la centena podemos elegir el 1, el 5 o el 9. Para la decena podemos elegir entre dos de ellos(porque ya utilizamos el primero en la centena), y para la unidad queda uno solo. Así 3 posibilidades para el primer lugar, 2 para el segundo y 1 para el tercero... son 3 * 2 * 1 = 6. Entonces podemos organizar los tres números de seis maneras distintas.

-------------------------------------------

A esta multiplicación (3 * 2 * 1)  se la llama factorial de un número (en este caso factorial de 3) y se escribe n! (en este caso 3!). Por convención se define que el factorial de 0 es 1. Es decir 0! = 1.
Conceptualmente es la permutación de n elementos. Es decir que:

P_n = n! = n * (n-1) * (n-2) * (n-3) * ... * (n-n+1)

-------------------------------------------

Ejemplo 1:
¿De cuántas maneras distintas pueden sentarse 4 personas en 4 lugares libres?

Esto es la permutación de 4 elementos.

P₄ = 4! = 4 * 3 * 2 *1 = 24

Rta: Pueden sentarse de 24 maneras diferentes.

-------------------------------------------

Ejemplo 2:
Si en un cd hay 10 canciones grabadas y quisiera escucharlas en distinto orden cada día. ¿Cuántos dias pasarán hasta que vuelva a repetirse la serie de canciones?

Esto es la permutación de 10 elementos.

P₁₀ = 10! = 10 * 9 * 8 * 7 * 6 * 5 * 4 * 3 * 2 *1 = 3628800

Rta: Pasarán 3628800 días antes de repetir una serie.

-------------------------------------------

Luego, habrá 8 ternas con 6 posibles permutaciones cada una, Por lo tanto habrá 48 ternas utilizables para armar el "Sudoku" básico. Un ejemplo:

Ejercicio: Armar dos Sudoku para completar, colocando sólo 3 datos en la matriz.

Expo Técnica 1 - Dock Sud

Durante los días 6 y 7 de noviembre del corriente año se realizó la exposición promocional que anualmente organiza la EET n° 1 de Dock Sud, Avellaneda, Buenos Aires.
Uno de los trabajos destacados de la Institución es la inclusión de un séptimo año puramente práctico, donde alumnos y docentes realizan proyectos anuales. El proyecto actualmente en ejecución es la reparación y puesta en marcha de varias computadoras a las que se les instala un sistema operativo y se agregan programas que realizan los alumnos. Dichos programas son juegos interactivos para niños de edad preescolar (totalmente desarrollados por alumnos). En este caso, se acordó la donación de lo antedicho al jardín de infantes vecino a la Institución, una vez finalizados los trámites de registro para permitir la distribución. Para mas información, puede llamar al teléfono 42038006.
Aprovecho la ocasión para mostrar algunos trabajos que expusieron distintos cursos.

Proporciones (3°)

Veremos de qué hablamos al decir proporción...
Si tenemos un triángulo cualquiera con vértices A, B y C y trazamos un segmento D-E que sea paralelo a B-C (interior al triángulo) notaremos algunas relaciones, veamos un ejemplo:

Utilizando GeoGebra medir es más fácil...

(hacer click en la imagen para agrandar)

De este ejemplo resulta ser que al dividir las longitudes los dos segmentos en los que se dividió A-B (es decir A-E=2.49 y E-B=1.51) y al dividir los del lado B-C (o sea B-D=4.77 y D-C=2.89) el resultado es el mismo, 1.65 (redondeado a dos decimales).

A partir de este ejemplo, se pide realizar en GeoGebra un triángulo, trazar la paralela a uno de sus lados, medir cada segmento y verificar que los resultados de las divisiones serán iguales. También deben medir los segmentos paralelos y explicar lo que sucede. Todo debe estar en la carpeta para seguir avanzando en clase.

Saludos.

En GeoGebra (3°)

Estimados alumnos, comenzamos a trabajar en GeoGebra.
Para algún remolón que todavía no descargó el programa, en este mismo blog pueden encontrar el enlace a la página oficial. Busquen el título en la columna de la derecha, en el mes de Marzo. Recuerden que es un software libre y gratuito por ser educativo.

Trabajaremos con los contenidos dados en las últimas clases (funciones trigonométricas)

Consignas:
1. Hacer la circunferencia trigonométrica (de radio 1)
2. Colocar un punto sobre la circunferencia (de modo que se mueva sobre ella cuando la arrastremos con el ratón)
3. Trazar un segmento desde el centro hasta el punto móvil
4. Trazar la perpendicular al eje x que pase por el punto móvil
5. Trazar otro segmento que represente al cateto opuesto del ángulo que se forma (se verá sobre la perpendicular anterior)
6. Editar el aspecto del cateto (haciendo doble clic sobre el mismo)
7. Hacer invisible la perpendicular (clic en la bolita que está a la izquierda de la fórmula en el espacio reservado al álgebra, columna izquierda)
8. Colocar el ángulo que forma el segmento móvil con el eje x y editarlo para que quede más grande

Finalmente guardar el ejercicio con el nombre de ustedes en un pendrive para verlo en clase o enviarlo a rcejas7@abc.gob.ar
Debería quedar algo así...

Todo lo que se pide fue visto en diferentes clases durante el año. Si no recuerdan algo, a buscar en la carpeta.
 La mejor manera de aprender es haciendo, asique manos a la obra.

Funcionamiento del sextante y del GPS (3°)

Les dejo un poco más de información

En la medición de la altura de un astro se coloca el sextante perpendicularmente y se orienta el instrumento hacia la línea del horizonte. Acto seguido se busca el astro a través de la mira telescópica, desplazando el espejo móvil hasta encontrarlo. Una vez localizado, se hace coincidir con el reflejo del horizonte que se visualiza directamente en la media parte del espejo fijo. De ese modo se verá una imagen partida, en un lado el horizonte y en el otro el astro. A continuación se hace oscilar levemente el sextante (con un giro de de muñeca) para hacer tangente la imagen del horizonte con la del sol y de ese modo determinar el ajuste preciso de ambos. Lo que marque el limbo será el ángulo que determina la Altura Instrumental u Observada de un astro a la hora exacta medida al segundo. Tras las correcciones pertinentes se determina la Altura Verdadera de dicho astro, dato que servirá para el proceso de averiguar la situación observada astronómicamente

Fuente: http://www.nulladiessinnemeditatione.com/el_sextante.htm

Quienes estén interesados en conocer un poco más sobre estos instrumentos pueden acceder a este enlace.

Para entender mejor el funcionamiento del GPS pueden visitar esta página, donde explican detalladamente la triangulación de los satélites -que expliqué en la última clase-.

Partiendo de todo lo anterior, conluimos que estos instrumentos trabajan relacionando datos de triángulos y repasamos las relaciones que permiten conocer algún lado o algún ángulo de un triángulo rectángulo a partir de conocer los otros dos (lados o ángulos). Escriban en sus carpetas las relaciones repasadas.

Finalmente presenté nuevas realaciones que combinan a las antedichas y permitirán resolver otro tipo de problemas relacionados a los triángulos rectángulos.
Ellas son las funciones SENO, COSENO y TANGENTE. Pedí finalmente que busquen en libros o en internet cuáles son las relaciones que analizan esas funciones. Responder entonces:
1. ¿Qué lados del triángulo rectángulo relaciona la función SENO?
2. Utilizando una calculadora científica diga: ¿cuál es el valor mínimo que da el seno de un ángulo? (prueben con distintos valores de ángulos utilizando la tecla "sin", por ejemplo: [sin] 45)
3. Del mismo modo: ¿cuál es el valor máximo?
4. ¿En qué ángulos se dan los resultados anteriores?

Averiguar... (3°)

Hola a todos.
Volvemos a trabajar luego de varios repasos de temas anteriores. En esta oportunidad se solicita que hagan unas averiguaciones (pseudo investigación) sobre el SEXTANTE y el GPS.

Para cada uno:
1. ¿Qué es?
2. ¿Para qué sirve?
3. ¿Cómo se obtiene la información?
4. Representación gráfica que explique la respuesta 3.


Este trabajo será evaluado.

Saludos.

Ejercicios (1°)

Realicen para el jueves los siguientes ejercicios, serán evaluados.

1. Un reloj atrasa 2 minutos cada hora ¿cuántos minutos atrasará en un día?
2. Un automóvil recorre 120 km con 32 litros de gasolina. ¿Cuántos litros necesita para recorrer 213 km?
3. Si un ciclista recorre 105 km en 3 horas. ¿Cuántos kms recorrerá en 13 min?


Ahora se pide interpretar lo que dice el enunciado y resolver

4. Un número más el siguiente es igual a 15 ¿Cuál es el número buscado?
5. Manuel tiene cierta edad. Cecilia tiene 2 años más que Manuel.
    Si suman ambas edades el resultado es 18. ¿Cuántos años tienen Manuel y Cecilia?
6. Andrés tiene cierta cantidad de estampillas. Marcelo tiene 6 estampillas menos que Andrés.
    Si se suman las estampillas de ambos jóvenes resultan 24 estampillas.
    Determinar cuántas estampillas tiene cada uno.

Potencias (repaso)

Se llama potencia de un número al exponente (superíndice) que posee un número o una letra (llamados base). Aclaramos con dos ejemplos de cada uno:

6² → (seis al cuadrado)               x³ → (equis al cubo)

3⁵  → (tres a la quinta)               x⁶ → (equis a la sexta)

Así cuando vemos un número o letra con exponente (por ahora veremos sólo exponentes pertenecientes al conjunto de los números naturales), sabremos que se trata de la multiplicación del número o letra de base. Utilizando los mismos ejemplos:

6² = 6 . 6 → (seis por seis)
 x³ = x . x . x → (equis por equis por equis)

3⁵ = 3.3.3.3.3 → (tres multiplicado 5 veces)
x⁶ = x.x.x.x.x.x → (equis multiplicado 6 veces)

Ya podemos generalizar y nombrar cada parte:

a^m = a.a.a.a. ... .a → (a es la base y m es el exponente)

(se multiplica la base tantas veces como indica el exponente)

CUIDADO:

TODO NÚMERO (o letra) ELEVADO A LA POTENCIA 0 (cero) ES IGUAL A 1 (uno)

3⁰ = 1           9⁰ = 1        1538⁰ = 1        x⁰ = 1      en general: a⁰ = 1

Propiedades

1. En la multiplicación de potencias de igual base, se suman los exponentes → a^m . aⁿ = a^{m + n}
2. En la división de potencias de igual base, se restan los exponentes ......... → a^m : aⁿ = a^{m - n}
3. Potencia de potencia, se multiplican los exponentes ............................... → (a^m)ⁿ = a^{m . n}



Gráfica de una función lineal

Hace algunos meses aprendimos cómo representar puntos en el plano cartesiano. También vimos que uniendo dos puntos dados queda representado un segmento de recta del cual supimos medir su longitud (utilizando el teorema de Pitágoras).
Lo que haremos ahora es casi lo mismo, incluso más sencillo ya que no vamos a medir longitudes.

Retomando el ejemplo dado en el artículo "función lineal" donde generamos una tabla, ahora cada uno de los datos de la tabla será representado en el plano como pares ordenados, así colocamos los pares (1,8); (2,13); (3,18); (4,23) :

x	y = 5x+3
1	8
2	13
3	18
4	23

Luego unimos los puntos con una recta y tenemos realizada la gráfica de la función dada.

Como ejercicio se pide realizar la gráfica de todas las funciones a las cuales armaron tablas (del artículo "función lineal")

Repaso de fracciones

Fracciones/Conjunto de los números Racionales

Una fracción es una parte de un total

Cortá una pizza en trozos, y tendrás fracciones:

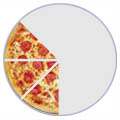1/2	1/4	3/8
(Una mitad)	(Un cuarto)	(Tres octavos)
El número de arriba te dice cuántas porciones quedan y el de abajo te dice en cuántas porciones se ha cortado la pizza.

Numerador / Denominador

Al número de arriba lo llamamos Numerador, es el número de partes que tenés.
Al de abajo lo llamamos Denominador, es el número de partes en que se ha dividido el total.

Fracciones equivalentes

Algunas fracciones parecen diferentes pero en realidad son la misma, por ejemplo:

	4/8	=	2/4	=	1/2
	(Cuatro octavos)		(Dos cuartos)		(Una mitad)

Normalmente lo mejor es dar la respuesta usando la fracción más simple (1/2 en este caso). Eso se llama Simplificar o Reducir la fracción.

Hay tres tipos de fracciones:

las que el numerad < el denominad => son fracciones menores que 1 => son propias

las que el numerad > el denominad => son fracciones mayores que 1 => son impropias

las que al dividirlas nos da un número entero => son fracciones aparentes.

Saludos.

Función lineal (3°)

A partir del repaso realizado con ecuaciones, donde hay una incógnita (la conocida x) y esta debe tener un valor único el cual se debe encontrar, damos un paso más y ampliamos la mirada.
Una función lineal nos ayuda a predecir el comportamiento de algunas cosas de la realidad (cuando hay proporcionalidad directa). Por ejemplo imaginemos que nos venden un producto a razón de $5.- por kilogramo y además nos cobran la caja en la que nos dan el producto $3.-
Como sólo sabemos eso, en lugar de tener la ecuación igualada a un resultado la veremos igualada a otra variable (que llamaremos y), veamos de que manera:
antes:     5x + 3 = 23  esto se da si y sólo si compramos 4 kilos del producto (x=4)
ahora:    5x + 3 = y   entonces podremos predecir cuánto valen los kilos que querramos comprar más el valor de la caja.
¿Cómo se resuelve esto? fácil, generamos una tabla y le damos valores a x de la siguiente manera:

x	y = 5x+3
1
2
3
4

Luego resolvemos reemplazando la x con el valor dado.

Si  x = 1  (compramos 1 kilo) =>  y = 5 . 1 + 3 = 8  (valor 8 pesos)

Si  x = 2  =>  y = 5 . 2 + 3 = 13 y así irán completando la tabla...

x	y = 5x+3
1	8
2	13
3	18
4	23

Realizar una tabla para cada ecuación

• y = 4x - 2
• y = (1/3)x - 1
• y = (7/2)x + 3
• y = (9/3)x + 6 - 2

Regla de tres simple (1°)

A partir del repaso (post receso) donde vimos las unidades de medidas y sus conversiones, llegamos a utilizar la regla de tres. Esta herramienta nos permitirá solucionar gran cantidad inconvenientes cotidianos.
Como su nombre lo dice, es utilizada cuando tenemos tres datos, dos de los cuales pertenecen a una unidad de medida y el restante a otra unidad. Veamos un ejemplo simple:

Si un kg de papas vale $3.-, ¿cuánto tendré que pagar si llevo 5 kg.?
Hacemos la regla de tres y analizamos
   1 kg ___________ 3 $
   5 kg ___________ x                donde x = 5 kg . 3 $
                                                                      1 kg
en el numerador se multiplica y queda     x = 15 kg . $
                                                                      1 kg
se simplifica kg con kg y el resultado es  x = 15 $.
Se utiliza mucho en áreas como la química, la física y obviamente la aprendemos en matemática.

Resolver: (ejercicios del Prof. Andrés Luetich)

1. Para averiguar cuántos kilómetros recorría mi auto con un litro de nafta, antes de viajar a Santa Fe por la autopista, llené el tanque. Al llegar a la capital de la provincia volví a llenar el tanque de nafta. Para hacerlo tuve que cargar quince litros de nafta. Sabiendo que la distancia entre Rosario y Santa Fe es de 160 km, ¿cuántos kilómetros recorrió mi auto por cada litro de combustible consumido?
2. Cuando las legiones del ejército romano debían desplazarse hacia algún punto del Imperio —para imponer el orden o defender las fronteras— recorrían unos 35 km por día. Hay que tener en cuenta que casi todos los hombres viajaban a pie y cargando sus armas. ¿Cuántos días les tomaba a estos legionarios recorrer una distancia de 1050 km.? 
3. En las aerosillas del Cerro Catedral, a unos pocos kilómetros de la Ciudad de San Carlos de Bariloche, trasladar a un contingente de 100 personas desde la base del Cerro hasta el fin del último de sus tres tramos insume unos 60 minutos. Teniendo en cuenta que a un pasajero ese traslado le toma 40 minutos, ¿cuánto tiempo demorá en llegar hasta arriba un grupo de 40 personas?
4. Un empleado que trabaja 6 horas diarias recibe como salario $4800 por mes. El dueño de la fábrica le ha comunicado que la empresa aumentará su horario de trabajo en 2 horas diarias y el sueldo proporcionalmente. ¿Cuál será a partir de ahora su sueldo?

Pulgada - centímetro

La relación entre estas dos unidades de medida es la siguiente:

1 pulgada = 2,54 centímetros
¿pueden decir cuántas pulgadas son 10 centímetros?
 

La pulgada es la unidad de medida que se usa oficialmente en tres países (Estados Unidos, Liberia y Birmania) y extraoficialmente en varios más, en general son países de habla inglesa.

En nuestro país se utiliza el metro (del cual derivan las otras unidades), pero es bastante común el uso de la pulgada en muchos ámbitos. Algunos ejemplos son: las pantallas (televisor, lcd, monitor o netbook); la madera (en cualquier maderera se habla en pulgadas); llaves y herramientas de mecánica; tuberías (para agua y para gas); soportes de grabación; tablas de surf; llantas para todos los vehículos, y algunos casos más.

Es importante tener este conocimiento para poder realizar conversiones cuando sea necesario.

Ejemplo:
Si alguien va a comprar los tirantes de madera para hacer un techo de 4 metros de largo, puede pasar que le digan "lleve de 2x6x4,20", pero el comprador puede pensar que son centímetros. Aquí se mezclan las unidades de medida y se supone que es para facilitar el trabajo. La primer parte (2x6) se refiere al ancho y el alto del tirante y son pulgadas, mientras que 4,20 se refiere a los metros de largo que tiene el tirante.

Ejercicio:
Convertir las medidas del tirante a centímetros.

 

Proyecto (1°)

Mientras comentaba sobre el proyecto que está armando tercer año, surgió la posibilidad de ser realizado también por primero. Para hacerlo democrático se votó en el aula alzando la mano para decidir si se realizaba o no. Pues la mayoría (14 votos positivos de 17 alumnos presentes) eligió hacerlo.
Las pautas a seguir son las mismas que se plantearon para tercer año pero sólo cambian los temas, que son los siguientes:
1) Teorema de Pitágoras
2) Clasificación de ángulos
3) La suma de los ángulos interiores de un triángulo es igual a dos rectos
4) Trazado de mediatrices y de bisectrices
Tienen tiempo para hacerlo hasta el 4 de julio, como acordamos en clase.

Saludos.

Semejanza (1°)

1) Dibujar dos triángulos rectángulos semejantes y otros dos que no lo sean.

2) Dibujar un triángulo isósceles con un ángulo de amplitud 120°. ¿Cuánto miden los otros dos ángulos? ¿Cuántos triángulos semejantes a éste se pueden hacer?

3) Si tenemos un triángulo ABC y trazamos el segmento DE paralelo a BC. Los dos triángulos que se forman ¿son semejantes? ¿Por qué?

Proyecto: "Video para la enseñanza"

Estimados alumnos, pongo a disposición de todos las pautas para la realización del proyecto.

1) El trabajo será realizado en grupos de dos, tres o cuatro alumnos.
2) El trabajo consta de una exposición, en formato de video, del tema (antes elegido) como si fueran profesores, alumnos, o cualquier otro personaje.
3) El guión es libre, pero siempre con respeto y sin comentarios que puedan herir la sensibilidad de quien lo vea.
4) La fecha de entrega es el 1 de julio (3° A) o 3 de julio (3° C)
5) Se permite la colaboración de padres, hermanos, etc.
6) Los trabajos serán evaluados desde dos perspectivas: producción y contenido.
7) Para la semana próxima deben presentar los nombres de los integrantes y el tema elegido por el grupo.
8) Los temas propuestos para desarrollar son los siguientes:
          a) Ángulos inscritos en la circunferencia
          b) Teorema de Thales
          c) Semejanza de triángulos
          d) Puntos notables en triángulos
          e) Función lineal
          f) Pasaje de números decimales a fracción y viceversa
          g) Tema a elección (consultar conmigo el que elijan)

Pueden consultar dudas o inquietudes por este medio.
Saludos ¡¡¡espero buenos trabajos!!!

Clasificación de triángulos

La clasificación de triángulos nos ayuda a interpretar situaciones en las cuales la deducción tiene mas importancia o urgencia que la toma de medidas (si no tenemos nada a mano como para medir).
Es muy importante saber esto para trabajos geométricos en toda la escuela secundaria.

Primero debemos saber que hay dos tipos de clasificación: SEGÚN SUS LADOS y SEGÚN SUS ÁNGULOS

SEGÚN SUS LADOS:
1) triángulo equilátero (todos sus lados de igual longitud)
2) triángulo isósceles (dos lados iguales y uno diferente)
3) triángulo escaleno (todos sus lados son de distinta longitud)

Ejemplos:

SEGÚN SUS ÁNGULOS
1) triángulo acutángulo (sus tres ángulos son agudos)
2) triángulo rectángulo (tiene un ángulo recto)
3) triángulo oblicuángulo (tiene un ángulo oblícuo)

Ejemplos:

Saludos, profe RJC.

semejanza de triángulos (1° y 3°)

Para determinar si dos triángulos son semejantes, pueden utilizar alguno de los criterios que se detallan a continuación ya que a simple vista no se debe.

Criterio A - A - A (ángulo - ángulo - ángulo): Dos triángulos son semejantes si tienen al menos dos ángulos iguales.

A = A´                    B = B´          en consecuencia C = C´

Criterio L - L - L (lado - lado - lado): Dos triángulos son semejantes si tienen los tres lados proporcionales.

a   =  b   =  c
a´      b´     c´

Criterio L - A - L: Dos triángulos son semejantes si tienen dos lados proporcionales y el ángulo comprendido entre ellos igual.

B = B´                           a   =  c
                                      a´     c´

(imágenes tomadas de http://www.vitutor.com/geo/eso/ss_3.html)

Busquen en un diccionario la definición de proporcionalidad y escríbanla en la carpeta.

Saludos, profe RJC.

En la circunferencia (3°)

Dejo este ejercicio para que copien en la carpeta e intenten resolver. Quien lo haga se gana un diez.
1) Dibujar una circunferencia de centro O y radio OA (el radio puede tener cualquier medida)
2) Trazar un diámetro AB a la circunferencia
3) Marcar un punto C en cualquier lugar del perímetro de la circunferencia
4) Unir los puntos para que se forme un triángulo
          Quedará algo parecido a esto, no necesariamente igual

5) Averiguar con alguna estrategia geométrica la amplitud del ángulo C

Angulos en la circunferencia (3°)

Les adelanto información del tema que veremos a partir de la semana próxima.
Elementos de la circunferencia:

• O es el centro de la circunferencia
• OT, OQ y OB son radios de la circunferencia
• AB es una cuerda de la circunferencia
• QT es un diámetro de la circunferencia
• L1 y L2 son rectas secantes a la circunferencia
• L3 es una recta tangente a la circunferencia
• El ángulo "alfa" es exterior a la circunferencia
• El ángulo "beta" es interior a la circunferencia

Embaldosado o Teselado (1°)

¿De qué habla el profe?
El título se refiere a figuras planas regulares (un tema que ya vimos) que al hacer coincidir sus lados y hacer compartir un vértice (de cada una), pueden cubrir una superficie sin dejar espacios en blanco ni encimarse una con otra. Por ejemplo la cerámica que ven en los pisos (antes las llamaban baldosas) o el panal de abejas.
Veamos algunos ejemplos:

Para el jueves les pido que busquen algún embaldosado en revistas o en internet y lleven a clase para comenzar a trabajar con ellos. No es necesario que lo impriman, pueden hacerlo en la carpeta.

Puntos en el plano (3°)

Ya hemos aprendido a ubicar puntos en el plano y a medir distancias entre puntos.
Faltaron ver algunos detalles, veamos:
Los ejes cartesianos dividen al plano en cuatro sectores llamados cuadrantes:
    El cuadrante I es el que cumple que todos sus puntos tienen ambas coordenadas positivas [ej. (2;4)]
    El cuadrante II es que tiene valores de x negativos y valores de y positivos [ej. (-3;1)]
    El cuadrante III es el que todos sus puntos tienen ambas coordenadas negativas [ej. (-7;-5)]
    El cuadrante IV es que tiene valores de x positivos y valores de y negativos  [ej. (3;-4)]

Propongo un ejercicio para hacer en carpeta.
Marcar el punto (2;3). Medir la distancia pitagórica hasta el orígen de coordenadas (0;0).
Encontrar todos los puntos del plano que tienen misma distancia al orígen que el punto dado.

Tutorial GeoGebra

Estimados alumnos, les dejo un enlace a un tutorial de GeoGebra para que comiencen a practicar.
Próximamente se enviarán trabajos para realizar con este programa. La geometría dinámica permitirá una mejor comprensión.
Tutorial GeoGebra

Saludos, profesor RJC.

Trazas con regla y compás (3°)

En virtud de las dificultades que noto para la construcción de perpendiculares y bisectrices, les dejo dos videos para que los miren las veces que crean necesarias hasta poder hacerlo correctamente.

Perpendicular a un segmento dado

Bisectriz y mediatriz

En este último enlace se repite el procedimiento para realizar la perpendicular que pasa por el punto medio del segmento dado, la cual se llama mediatriz.

Practiquen estos procedimientos con los ejercicios que están publicados desde la semana anterior.

Definiciones geométricas (1° a 6°)

Les dejo algunas definiciones importantes para la geometría plana.

Punto: Es lo que no tiene partes (se representa geométricamente para hacer referencia)

Recta: Es una sucesión indefinida de puntos en una misma dirección. No tiene ni principio ni final.

Semirrecta: Es una línea recta que tiene principio pero no final.

Segmento: Es la parte de una recta comprendida entre dos puntos.

Rectas secantes: Dos rectas son secantes cuando tienen un punto en común (se cruzan en un punto).

Rectas paralelas: Dos rectas son paralelas cuando no tienen ningún punto en común (nunca se cruzan).

Rectas coincidentes: Dos rectas son coincidentes cuando tienen todos sus puntos en común.

Rectas perpendiculares: Dos rectas son perpendiculares cuando al cortarse forman cuatro ángulos iguales de 90º.

Mediatriz: Es el segmento perpendicular a un segmento dado, que pasa por el punto medio del mismo.

Vértice: Es el punto donde dos o más rectas se cruzan.

Ángulo: Es cada una de las porciones en que queda dividido el plano cuando se cruzan dos rectas secantes.

Ángulo agudo: Es un ángulo menor de 90º.

Ángulo recto: Es un ángulo de 90º.

Ángulo obtuso: Es un ángulo mayor de 90º.

Bisectriz: Es la recta que al pasar por el vértice de un ángulo dado, lo divide en dos partes exactamente iguales.

Polígono: Un polígono es una porción de plano limitada por tres o más líneas rectas no paralelas entre sí. Los laterales del polígono se llaman lados y el punto donde se cruza cada par de rectas se llama vértice. Puede ser regular o irregular.

Polígono regular: Es un polígono que tiene todos sus lados y todos sus ángulos iguales.

Polígono irregular: Es un polígono que no tiene ni todos sus lados ni todos sus ángulos iguales.

Diagonal: Es el segmento de recta, comprendido entre dos vértices no consecutivos de un polígono de cuatro o más lados.

Altura: Es la distancia entre un lado de un polígono y el vértice opuesto, en dirección perpendicular.

Triángulo: Es un polígono de tres lados.

  Triángulo equilátero: Es un triángulo que tiene los tres lados iguales.

  Triángulo isósceles: Es un triángulo que tiene dos lados iguales y uno desigual.

  Triángulo escaleno: Es un triángulo que tiene los tres lados desiguales.

  Triángulo acutángulo: Es un triángulo que tiene los tres ángulos agudos.

  Triángulo rectángulo: Es un triángulo que tiene un ángulo recto y los  otros dos agudos.

  Triángulo obtusángulo: Es un triángulo que tiene un ángulo obtuso y los otros dos agudos.

Apotema: Es el segmento de recta que va desde el centro de un polígono regular al punto medio de uno de sus lados.

Polígonos regulares (1°)

En clase les comenté que las figuras planas que están formadas por segmentos de recta se llaman polígonos. Y en particular, cuando esos segmentos (que llamamos lados) tienen la misma longitud, se llaman polígonos regulares. Veamos algunos ejemplos...

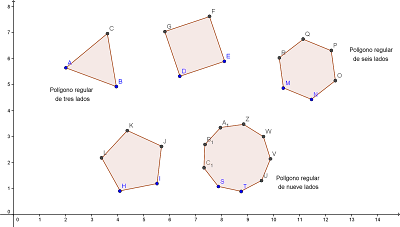
Además armamos una tabla que deben completar. Aquí va la ayuda para la columna "Valor del ángulo interior".
Ya sabemos cuánto suman los ángulos interiores de cualquier triángulo (180°). Entonces, si pudiéramos dividir cualquier polígono en triángulos, podríamos analizarlos mejor, vean cómo se hace con el polígono MNOPQ de seis lados (también llamado hexágono):

Al unir los vértices formamos 4 triángulos, si cada uno suma 180°, entonces 180° x 4 = 720°. Y como la figura tiene 6 lados, decimos 720° / 6 = 120°. Con el mismo procedimiento lograrán averiguar cuánto miden los ángulos interiores de los demás polígonos. De esa manera completarán la columna indicada con los valores correspondientes.
Se pide que copien este ejemplo en la carpeta y que durante la clase del jueves 25/4 realicen lo indicado.

Saludos del profesor     

Puntos notables en triángulos

Les dejo este enlace  donde encontrarán la teoría y ejercicios respecto al tema Puntos Notables.

Lean la teoría y realicen todos los ejercicios propuestos en hoja aparte para ser evaluados.

En la página que aquí se enlaza pueden ver la ubicación de cada punto en un triángulo al que podrán cambiar forma y tamaño para una mejor interpretación.

Perpendiculares y bisectrices (3°)

Estuvimos viendo como trazar la perpendicular que pasa por el punto medio de un segmento dado.
Luego vimos como hacerlo con los segmentos que forman un triángulo. Dichas perpendiculares se cruzan en un punto y ustedes averiguarán cómo se llama ese punto. Además ¿cómo se llaman esas perpendiculares construidas?
En el siguiente enlace se muestra como se hacen paso a paso: Perpendiculares

También vimos como trazar las bisectrices de los ángulos del triángulo y ustedes averiguarán cómo se llama la triple intersección de las bisectrices. ¿Cómo se llaman esos segmentos?
Ahora les pediré que a otro triángulo le ubiquen los puntos medios de sus lados y tracen los segmentos que unen cada punto medio con el vértice opuesto. Averigüen cómo se llama ese punto de intersección. ¿Cuál es el nombre de los segmentos trazados?

Aún no les dije como trazar la perpendicular a un segmento que pase por un determinado punto exterior a ella (al hacerlo en un triángulo, donde se traza la perpendicular a cada segmento que pasa por el vértice opuesto se llama "altura"). Lo veremos la próxima clase, pero igualmente los desafío a investigar, sorprenderme, intentar hacerlo ustedes mismos y ganarse una buena nota.

Ángulos (1°)

Antes de ir a los ejercicios, recordemos que los ángulos pueden ser AGUDO, RECTO u OBLÍCUO ¿qué es lo que define esa clasificación?

Les propongo que realicen las siguientes figuras ayudándose con el transportador y la regla:

a) Un triángulo que tenga un ángulo interno de 40°, otro de 50°. El restante ángulo deberán medirlo para conocerlo. ¿Cuánto suman los tres ángulos? (Ayuda)

b) Otro cuyos ángulos internos sean de 50°, 60° y el último lo miden ustedes. ¿Cuánto suman los tres?

c) Otro triángulo al que ustedes pondrán los grados que decidan. ¿Cuánto suman los tres?

d) Finalmente hagan un triángulo sin importar la forma y midan los tres ángulos internos. ¿Cuánto suman? ¿Encontraron alguna coincidencia?

Además de hacer los ejercicios, les pido que repasen ángulos complementarios y ángulos suplementarios ya que lo necesitarán para las próximas clases.

El número de Euler (1°)

Estudiaremos algunos cuerpos geométricos para deducir la relación de Euler. En la carpeta deben copiar la tabla (que completaremos el jueves en clase), dibujar el tetraedro y el cubo y luego armar con papel o cartulina el octaedro, el dodecaedro y el icosaedro. Los mejores constructores tendrán nota de premio.

	N° de caras (c)	N° de vértices (v)	N° de aristas (a)	N° de Euler= c+v-a
Tetraedro	4	4		2
Cubo	6	8	12
Octaedro
Dodecaedro
Icosaedro

Las figuras pueden verlas en un libro o en internet simplemente colocando el nombre en un buscador.